JavaScript Chess AI (Part 3)
Welcome to part 3 of creating a Chess AI! Today’s blog post is a really exciting one – we’ll be implementing the minimax algorithm with alpha-beta pruning to give our AI chess agent the ability to consider moves in the future. This will have immediate benefits for our agent’s chess ability, although as we’ll see, without proper evaluation the agent will still play quite poorly. We’ll cover evaluation improvements in the next blog post.
If you are just joining in, you can read the previous parts of this blog series below:
Acknowledgements
As always, some acknowledgements! First, this YouTube explanation of minimax by Sebastian Lague is nothing short of brilliant, and the LinkedIn Learning course I took on “AI Algorithms for Gaming” (see LinkedIn Learning certificates) was also extremely helpful. Finally, as always, the chess programming wiki was super helpful for implementing these algorithms for chess.
Search and Evaluation
Search and Evaluation lie at the heart of a good chess engine. Search refers to the process of iteratively examining future moves, countermoves, countermoves to those moves, and so on, and evaluating the resulting positions to determine what the best move is. For this, we use the minimax algorithm, which finds the best move for the current player, assuming optimal play from the opponent. In general, the deeper the search, the better the moves are. Unfortunately, brute-force search is extremely computationally expensive, as the number of evaluated moves n grows exponentially (n^depth) as we go deeper into the future. For example, assuming 30 possible moves per position, the number of moves to consider for depth 2 is just 30^2 = 900, but for depth 5 is already 30^5 = 24,300,000. For this reason, it is very important to restrict or “prune” the search tree as much as possible. For this, we will use alpha-beta pruning, as you’ll see below.
Evaluation, on the other hand, refers to the process of considering a position on the board and deciding whether it is favorable for White or for Black. As we saw in part 2, a very simple way of evaluating a position is by counting up the values of pieces for both sides. Of course, as any good chess player knows, there is so much more to a strong position than piece values: center control, active pieces, king safety, passed pawns, etc. For today we will stick with our simplified chess evaluation function, however, but we will drastically improve it in part 4. For now, I will just focus on the search algorithm.
The Minimax Search Algorithm
The minimax algorithm works by iterating through various moves and countermoves in a search tree and finding the best guaranteed final position assuming the maximizer always chooses the best option in a given position and the minimizer the worst possible position (for the maximizer). In other words, if it is White to play, White will choose the move that guarantees the best possible final position, assuming that Black (the minimizer in this case) always chooses the moves that are worst for White. More concretely, the algorithm will dive into the search tree to some predetermined depth (AKA depth-first search), and evaluate all the possible board positions at that depth via some evaluation function. The evaluation of earlier (parent) board states are simply equal to the maximum (or minimum) of all next (child) board states, depending on whose turn it is.
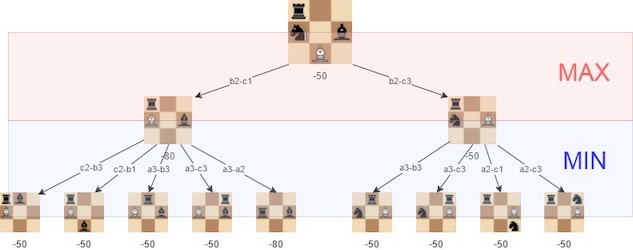
Minimax Example
Suppose White has 2 possible moves: c4 and Nxf3. The first just moves a pawn, and results in a position of totally piece equality (score = 0), while Nxf3 wins Black’s queen (score = +9). Which move should White choose? Before we decide, we need to consider Black’s possible counter moves. If White goes c4, the position is guaranteed to still be equal (score = 0) no matter what Black does. If White goes Nxf3, Black has two choices: a3 and Rh1++. The first just moves a pawn and maintains the favorable score for White (+9), but the second option delivers checkmate (score = -999 in total favor of Black)! Given that, what is the real value of Nxf3? Is it really +9? No it isn’t! Assuming Black always chooses the move that is worst for White (in this case delivering checkmate, resulting in a board evaluation of -999), the real value of Nxf3 is -999, not +9. White should choose the move c4, the move that minimizes the maximum loss. Sure +9 would be possible if Black went a3, but we will always assume Black plays perfectly, thus we need to minimize the loss, not maximize the potential score.
The reason minimax is called that is because it MINImizes the MAXimum loss one can expect. In other words, it finds the move that guarantees the best possible board condition, assuming the opponent is always going to play the best possible countermove.
Minimax Code
With that understanding in place, let’s take a look at the JavaScript implementation of the minimax algorithm.
function minimax(position, depth, maximizing_player){
// if terminal state (game over) or max depth (depth == 0)
if (position.in_checkmate() || position.in_draw() || depth == 0){
return evaluatePosition(position);
}
if (maximizing_player) {
// find move with best possible score
let maxEval = -Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let childEval = minimax(position, depth - 1, false)
maxEval = Math.max(maxEval, childEval);
position.undo()
}
return maxEval;
} else {
// find move with worst possible score (for maximizer)
let minEval = +Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let childEval = minimax(position, depth - 1, true)
minEval = Math.min(minEval, childEval)
position.undo()
}
return minEval;
}
}
Let’s go through each line carefully to make sure everything is clear.
minimax(game, 3, true)
First, the minimax algorithm gets called for the player making a move. For example, if it is White to play, we would call the minimax function with a depth of 3 as above. Notice that maximizing_player is set to true, since White wants the maximum possible board evaluation.
if (position.in_checkmate() || position.in_draw() || depth == 0){
return evaluatePosition(position);
}
Next, within the function, we first check whether we have reached the maximum depth or if the position is terminal. If either of these are the case, we return the evaluation of the position. As mentioned previously, the details of how these positions are evaluated are important, but for now we’ll assume that we just sum the values of the White pieces and subtract the values of the Black pieces.
if (maximizing_player) {
// find move with best possible score
let maxEval = -Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let childEval = minimax(position, depth - 1, false)
maxEval = Math.max(maxEval, childEval);
position.undo()
}
return maxEval;
}
Next, since White is the maximizing player, we consider all possible moves (let possibleMoves = position.moves();), then loop through each possible move. For each move, we need to consider the counter move from Black. To do this, we call the minimax function again, but this time set maximizing_player to false via let childEval = minimax(position, depth - 1, false), since Black is the minimizing player. We also set depth = depth - 1, such that the subsequent recursive minimax call will have a depth of 2.
} else {
// find move with worst possible score (for maximizer)
let minEval = +Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let childEval = minimax(position, depth - 1, true)
minEval = Math.min(minEval, childEval)
position.undo()
}
return minEval;
}
In the subsequent minimax function call, maximizing_player is now false, so we go into the second half of the if statement. Here we again loop through all possible moves (this time, Black’s moves). To evaluate these moves we again have to consider all of White’s countermoves, and next Black will choose the move with the lowest value. So, we again call the minimax function recursively for each move, and this time set maximizing_player back to true, reducing depth by 1 again. Notice here that we are finding the minimum possible value (starting with +Infinity), rather than finding the maximum possible value.
We continue this process until depth == 0 during a minimax call. Here, finally, we return the evaluation of the given position. This evaluation gets fed backwards up the chains, until eventually a decision is made at the earliest minimax function call.
Minimax Code (ACTUAL)
One detail that I omitted in the code above (for readability) is that we also want to keep track of the best move for a current position, not just its evaluation. That will allow us to then execute the best move at the highest level of iteration. The final code for the minimax algorithm is therefore as follows:
function minimax(position, depth, maximizing_player){
// if terminal state (game over) or max depth (depth == 0)
if (position.in_checkmate() || position.in_draw() || depth == 0){
return [null, evaluatePosition(position)];
}
let bestMove;
if (maximizing_player) {
// find move with best possible score
let maxEval = -Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let [childBestMove, childEval] = minimax(position, depth - 1, false)
if (childEval > maxEval) {
maxEval = childEval;
bestMove = possibleMoves[i]
}
position.undo()
}
return [bestMove, maxEval];
} else {
// find move with worst possible score (for maximizer)
let minEval = +Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let [childBestMove, childEval] = minimax(position, depth - 1, true)
if (childEval < minEval) {
minEval = childEval;
bestMove = possibleMoves[i]
}
position.undo()
}
return [bestMove, minEval];
}
}
As you examine the code above, notice that we return the move null in the terminal state, since there are 0 moves being considered for these states. We also can retrieve the best move of the various children board positions (childBestMove), but ultimately we do not use these, since we are concerned with the best move in THIS position, not possible subsequent ones.
And with that, we have an effective way of evaluating future states in our chess game! All that is left is to make sure we have an evaluation function for a given position, as follows. This again makes use of several methods of the chess.js Class, such as .in_checkmate() and .in_draw().
function evaluatePosition(position){
if (position.in_checkmate()){
return (position.turn() == 'w') ? -checkmate_eval : checkmate_eval;
} else if (position.in_draw()){
return 0;
} else {
return evaluateBoard(position.board());
}
}
Our evaluateBoard function will be the same as in the last blog post, as follows. This will be our main area of improvement in future versions of the AI, stay tuned!
function evaluateBoard(board){
let evaluation = 0;
for (let i = 0; i < 8; i++) {
for (let j = 0; j < 8; j++) {
evaluation += getPieceValue(board[i][j])
}
}
return evaluation;
}
Finally, we can make a move for the AI by calling the minimax function on its turn.
function makeMinMaxMove(){
let maximizing = (game.turn() == 'w');
let [bestMove, bestEval] = minimax(game, 3, maximizing);
game.move(bestMove);
board.position(game.fen())
removeRedSquares();
updateStatus();
}
We can call this function every time we have finished making move, during the onDrop event.
function onDrop(source, target){
removeGreySquares();
let move = game.move({
from: source,
to: target,
promotion: 'q' // NOTE: always promote to a queen for example simplicity
})
if (move == null) return 'snapback'
removeRedSquares();
updateStatus();
// make best move for Black via min max
setTimeout(makeMinMaxMove, 250);
}
With that, we are finished!
Alpha-Beta Pruning
Or are we? One thing you might notice is that I haven’t included a version of the minimax agent to play against. That is because minimax is a brute-force search algorithm. It will consider all possible countermoves to countermoves to countermoves, such that the number of states grows exponentially, as explained previously. This is incredibly slow, and the AI as is isn’t very fun to play against. For example, here is a break down of evaluation times while running this on my mac:
Depth 1:
let [bestEval, bestMove] = minimax(game, 1, maximizing);
Time to complete 21 iterations: 0.013 (s)
Depth 2:
let [bestEval, bestMove] = minimax(game, 2, maximizing);
Time to complete 421 iterations: 0.083 (s)
Depth 3:
let [bestEval, bestMove] = minimax(game, 3, maximizing);
Time to complete 9323 iterations: 1.065 (s)
Depth 4:
let [bestEval, bestMove] = minimax(game, 4, maximizing);
Time to complete 206,604 iterations: 23.751 (s)
Depth 5:
let [bestEval, bestMove] = minimax(game, 5, maximizing);
Time to complete 5,072,213 iterations: 649.963 (s)
As you can see, even a fairly narrow search of depth 5 takes over 10 minutes (!!!) and requires evaluating over 5 million different chess positions. Combined with our admittedly inefficient evaluation function (that counts up all the values of the pieces at each iteration, more on that in the next post), this proves to be quite the daunting computational task. Fortunately, there is a guaranteed improvement to the speed of the minimax algorithm: alpha-beta pruning.
Alpha-Beta Pruning Example
Consider our previous example again, where White had choices between c4 (leading to an equal position with score = 0) and Nxf3, leading to checkmate by Black on the next move. Suppose there was a third choice, Bb5, and White would like to consider this move as well. Bb5 gives Black two options (e6 and Nd4). Evaluating the first (e6), we find that the resulting position gives an evaluation of -1 slightly favorable to Black. Given that evaluation, consider whether or not we need to evaluate the remaining move for White in this position, Nd4. No matter what the evaluation in that position, -5, -1, 0, 5, etc, since Black is moving and will always choose the lowest number, Black is guaranteed a score of AT LEAST -1. If the evaluation of Nd4 is > -1, Black will always choose e6. If Black is guaranteed at least a -1, that means that the value of White’s initial move Bf4 is ALSO at least -1 (or worse). And since we already know that the move c4 guarantees a score of equality (0), White will never choose Bf4, regardless of the evaluation of the unchecked move Nd4, since Bf4 is guaranteed to lead to a worse position for White.
This is the essence of alpha-beta pruning. If we know that a branch is guaranteed to be worse than a previously confirmed branch, then we can stop evaluating it. Consider the example below, and you can see that even with few choice per branch this saves a lot of unnecessary computation. With 30 possible moves per branch as in chess, the saving are exponentially greater!
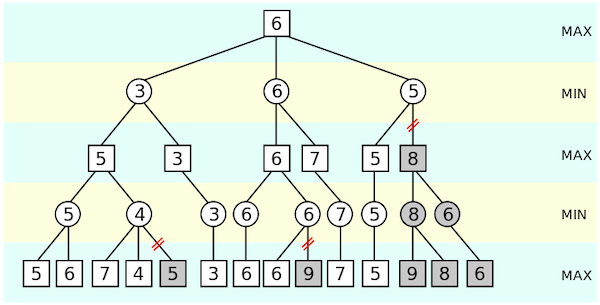
Alpha-Beta Code
With this in mind, let’s implement alpha-beta pruning for our chess agent! It is a simple extension of the minimax algorithm we already have. All we do is keep track what the best guaranteed position for White is (most positive) and what the best guaranteed position for Black is (most negative) in the alpha and beta parameters respectively. While we are looping through all of the moves in a given position, we continually check whether or not beta is less than or equal to alpha, and if it is, we break out of the loop (no longer consider other candidates) because we have already found at least one move in this state that means this state will never be visited.
The code for this is quite simple. First, we add alpha and beta as parameters to our minimax function:
function minimax(position, depth, alpha, beta, maximizing_player){
...
}
We can then call the function in our onDrop function as before:
function makeMinMaxMove(){
let maximizing = (game.turn() == 'w');
let [bestMove, bestEval] = minimax(game, 3, -Infinity, +Infinity, maximizing);
game.move(bestMove);
board.position(game.fen())
removeRedSquares();
updateStatus();
}
Notice how we initialize alpha to -Infinity and beta to +Infinity. In other words, the highest guaranteed score initially is -Infinity, so it is guaranteed to find the true highest possible score, even if that highest possible score is -1,000,000 or something.
The majority of the function is identical to previous minimax implementation we saw, but we add the following to both for loops that iterate through the moves in a given position:
For the maximizing player:
for (let i = 0; i < possibleMoves.length; i++) {
...
alpha = Math.max(alpha, childBestEvaluation)
if (beta <= alpha) {
break;
}
}
For the minimizing player:
for (let i = 0; i < possibleMoves.length; i++) {
...
beta = Math.min(beta, childBestEvaluation)
if (beta <= alpha) {
break;
}
}
To reiterate what will happen, let’s go back to our example. We are the White player, with moves c4 leading to an equal position, Nxf3 leading to checkmate, and an unevaluated Bf4 move. Since we’ve already established that c4 = 0 and Nxf3 = -999, alpha is currently equal to 0. In the code above, notice how alpha is always set to the maximum possible evaluation of its children via alpha = Math.max(alpha, childBestEvaluation). What happens next? We evaluate the first move for Black e6, and find its evaluation is -1. Beta is set to this value, and all of a sudden beta is less than alpha (-1 < 0). If this is the case, then Black’s best guaranteed move in this position is worse for White than the best evaluation guaranteed elsewhere. For this reason, we break out of the for loop.
Here is the final implementation of the minimax function, with alpha-beta pruning:
function minimax(position, depth, alpha, beta, maximizing_player){
// if terminal state (game over) or max depth (depth == 0)
if (position.in_checkmate() || position.in_draw() || depth == 0){
return [null, evaluatePosition(position)];
}
let bestMove;
if (maximizing_player) {
// find move with best possible score
let maxEval = -Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let [childBestMove, childEval] = minimax(position, depth - 1, alpha, beta, false)
if (childEval > maxEval) {
maxEval = childEval;
bestMove = possibleMoves[i]
}
position.undo()
// alpha beta pruning
alpha = Math.max(alpha, childEval)
if (beta <= alpha) {
break;
}
}
return [bestMove, maxEval];
} else {
// find move with worst possible score (for maximizer)
let minEval = +Infinity;
let possibleMoves = position.moves();
for (let i = 0; i < possibleMoves.length; i++) {
position.move(possibleMoves[i])
let [childBestMove, childEval] = minimax(position, depth - 1, alpha, beta, true)
if (childEval < minEval) {
minEval = childEval;
bestMove = possibleMoves[i]
}
position.undo()
// alpha beta pruning
beta = Math.min(beta, childEval)
if (beta <= alpha) {
break;
}
}
return [bestMove, minEval];
}
}
So, how much time does this save? A ton! Here is another breakdown for the time needed to complete evaluations at various depths:
Depth 1:
let [bestEval, bestMove] = minimax(game, 1, -Infinity, +Infinity, maximizing);
Time to complete 21 iterations: 0.013 (s)
Depth 2:
let [bestEval, bestMove] = minimax(game, 2, -Infinity, +Infinity, maximizing);
Time to complete 60 iterations: 0.035 (s)
Depth 3:
let [bestEval, bestMove] = minimax(game, 3, -Infinity, +Infinity, maximizing);
Time to complete 524 iterations: 0.127 (s)
Depth 4:
let [bestEval, bestMove] = minimax(game, 4, -Infinity, +Infinity, maximizing);
Time to complete 1413 iterations: 0.417 (s)
Depth 5:
let [bestEval, bestMove] = minimax(game, 5, -Infinity, +Infinity, maximizing);
Time to complete 12899 iterations: 2.33 (s)
If you recall, last time it took 649 seconds (over 10 minutes!) to run a depth 5 search. Here we did the same depth search in only 2.3 seconds. What is even better is that we are statistically guaranteed to get the same answer, since all we are doing is not searching moves that are unnecessary to calculate.
Final Modifications
As a final small tweak, we will also shuffle the moves in a given position. As explained in more detail below, move ordering is very important for alpha-beta pruning, and at the very least, this will prevent the chess computer from playing the identical game of chess against you every time you try it out. To shuffle, we’ll use the classic Fisher-Yates shuffle, shown below:
// Fisher-Yates shuffle
function shuffle(array){
for(let j, x, i = array.length; i; j = Math.floor(Math.random() * i), x = array[--i], array[i] = array[j], array[j] = x);
return array;
}
Then, all we do is shuffle the possible moves in a position, so that there is more variety in what gets played.
let possibleMoves = shuffle(position.moves());
Further Improvements
With that, we have arrived at the end of blog post 3! We have come a long way, but there is still tremendous room for improvement. First and foremost, our evaluation function is terrible. Not only is it terribly inefficient (recounting up all of the pieces in each possible position, even though from one move to another at most one piece can change), it is also just inaccurate. Next time we’ll see how to write a much more powerful evaluation function that considers things like center control, castling, active pieces, attacking chances, etc.
Second, there are many more techniques we could use to further increase the efficiency of the search algorithm. First, by move 2, any position we would like to search to depth 5 has already been searched to depth 3 when it was our turn last. It is a huge waste of computational time to recalculate these! To fix this, we can implement something called a transposition table, which checks whether a current position has been previously evaluated.
The next is move ordering. In our previous example, we were able to prune the Bf4 path because we previously saw that c4 guaranteed a better position. But what if we evaluated the Bf4 path first? Then we wouldn’t be able to prune anything, since by the time we discovered c4 eliminates the Bf4 path, we would have already evaluated it. It turns out that alpha-beta pruning can in fact prune almost 99% of moves, if they are evaluated from best to worst, but 0% of moves if they are evaluated from worst to best. Since we don’t know how good moves are before we order them, we can use some heuristics to guess which ones might be good. For example, captures that capture valuable pieces (say a Queen) are more likely to lead to good positions than captures of weaker pieces (like a pawn), so we might decide to evaluate those first. Likewise, checking moves might be evaluated before other moves, since they could win us the game.
Finally, we could also implement iterative deepening, so that we are not constrained by depth but rather by TIME. In positions with few moves, we might be able to go to depth 10 in the same time we could only go to depth 5 in another. If we always use the same depth, we lose out on this potential to make a great well-thought out move.
All of these things will be considered in future blog posts, time allowing. In the mean time, you can play the agent we have built below! Warning, it is already getting a lot better, be careful! ;) It uses a depth of 3.
